miércoles, 4 de mayo de 2011

Circunferencia Gonometrica

Circunferencia goniométrica

De Wikipedia, la enciclopedia libre
Parametrización de la circunferencia goniométrica. La variable t es el ángulo y sus puntos son: (x, y) = (cost, sent).
La circunferencia goniométrica, trigonométrica, unitaria o «círculo unidad» es una circunferencia de radio uno, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas cartesianas, de un plano euclídeo.
Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.
Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, x e y satisfacen la ecuación:
x^2 + y^2 = 1 = radio = hipotenusa \,

Contenido

[ocultar]

Razones trigonométricas en la circunferencia unidad

La circunferencia unidad y el triángulo rectángulo asociado.
Si (x, y) es un punto de la circunferencia unidad, y el radio que tiene el origen en (0, 0), forma un ángulo \alpha \, con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triángulos rectángulos auxiliares, de la siguiente manera:
El seno es la razón entre el cateto opuesto (a) y la hipotenusa (c)
\operatorname{sen}(\alpha)= \frac{a}{c}
y dado que la hipotenusa es igual al radio, que tiene valor = 1, se deduce:
\operatorname{sen}(\alpha)= a \,
El coseno es la razón entre el cateto adyacente (b) y la hipotenusa (c)
\cos(\alpha)= \frac{b}{c}
y como la hipotenusa tiene valor = 1, se deduce:
\cos(\alpha)= b \,
La tangente es la razón entre el cateto opuesto y el adyacente
\tan(\alpha)= \frac{a}{b}
Principales valores de las razones trigonométricas representados como segmentos respecto de la circunferencia goniométrica.
Valores de los ángulos más comunes y las coordenadas correspondientes sobre la circunferencia goniométrica.
Por semejanza de triángulos: AE / AC = OA / OC
como OA = 1, se deduce que: AE = AC / OC
\tan(\alpha)= segmento AE \,

Razones trigonométricas recíprocas

La cosecante, la secante y la cotangente, son las razones trigonométricas recíprocas del seno, coseno y tangente:
\csc (\alpha) = \frac{1}{\operatorname{sen} (\alpha)} = \overline{OF}
\sec (\alpha) = \frac{1}{\cos (\alpha)} = \overline{OE}
\cot (\alpha) = \frac{1}{\tan (\alpha)} = \overline{AF}
Los valores de la cotangente, la secante y la cosecante se obtienen, análogamente, mediante semejanza de triángulos.

Topología

En topología, a la circunferencia unitaria (también denominado círculo unitario) se la clasifica como S1; la generalización para una dimensión más es la esfera unidad S2.

Véase también

Publicado por Daniel.D en 0:42

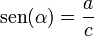
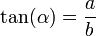
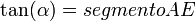
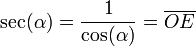
0 comentarios:

Publicar un comentario