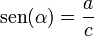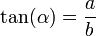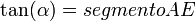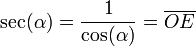Curcunferencia GoniometricaDaniel Domínguez Mascaraque, Creación realizada con GeoGebra |
skip to main |
skip to sidebar
Curcunferencia Goniometrica - GeoGebra Hoja Dinámica
La circunferencia goniométrica, trigonométrica, unitaria o «círculo unidad» es una circunferencia de radio uno, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas cartesianas, de un plano euclídeo.
Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.
Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, x e y satisfacen la ecuación:
 con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triángulos rectángulos auxiliares, de la siguiente manera:
con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triángulos rectángulos auxiliares, de la siguiente manera:
El seno es la razón entre el cateto opuesto (a) y la hipotenusa (c)

 Por semejanza de triángulos: AE / AC = OA / OC
Por semejanza de triángulos: AE / AC = OA / OC
como OA = 1, se deduce que: AE = AC / OC

Ampliación de matemáticas
Blog sobre el estudio de las matemáticas
jueves, 5 de mayo de 2011
miércoles, 4 de mayo de 2011
Circunferencia Gonometrica
Circunferencia goniométrica
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.
Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, x e y satisfacen la ecuación:
Contenido[ocultar] |
Razones trigonométricas en la circunferencia unidad
Si (x, y) es un punto de la circunferencia unidad, y el radio que tiene el origen en (0, 0), forma un ángulo con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triángulos rectángulos auxiliares, de la siguiente manera:
con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triángulos rectángulos auxiliares, de la siguiente manera:El seno es la razón entre el cateto opuesto (a) y la hipotenusa (c)

Principales valores de las razones trigonométricas representados como segmentos respecto de la circunferencia goniométrica.

Valores de los ángulos más comunes y las coordenadas correspondientes sobre la circunferencia goniométrica.
como OA = 1, se deduce que: AE = AC / OC
Razones trigonométricas recíprocas
La cosecante, la secante y la cotangente, son las razones trigonométricas recíprocas del seno, coseno y tangente:Topología
En topología, a la circunferencia unitaria (también denominado círculo unitario) se la clasifica como S1; la generalización para una dimensión más es la esfera unidad S2.Véase también
 Wikimedia Commons alberga contenido multimedia sobre Circunferencia goniométrica. Commons
Wikimedia Commons alberga contenido multimedia sobre Circunferencia goniométrica. Commons- Medida de ángulos
- Razones trigonométricas
miércoles, 13 de abril de 2011
jueves, 17 de febrero de 2011
Tipos de graficas de funciones
EJEMPLO DE FUNCION
Una función es una maquiníta en donde ponemos trozos de "pan" y de donde tomamos "tostadas". En este caso...
el pan se llama "variable independiente", porque podemos poner en la maquinita trozos de cualquier cantidad, siempre que sea esa cantidad "manejable" por la maquinita.
Lo que sale de la maquinita se llama "variable dependiente", porque el tama~no de la tostada depende de la cantidad del pan que hemos puesto.
Consecuentemente, podemos decir que una maquinita es una ecuación, pone cantidades de pan definidas iguales a cantidades específicas de tostadas.
miércoles, 9 de febrero de 2011
Estudio grafico de funciones
CONCEPTO DE FUNCIÓN
Una función es una relación o correspondencia entre dos magnitudes, de manera que a cada valor de la primera le corresponde un único valor de la segunda (o ninguno), que llamamos imagen o transformado.
A la función se le suele designar por f y a la imagen por f(x), siendo x la variable independiente.
* Variable independiente: la que se fija previamente
* Variable dependiente: La que se deduce de la variable independiente.
Las funciones son como máquinas a las que se les introduce un elemento x y devuelven otro valor y, que también se designa por f(x).
Por ejemplo, la función f(x) = 3x2 + 1 es la que a cada número le asigna el cuadrado del número multiplicado por 3 y luego sumado 1.
Así f(2) = 3*22 + 1= 3*4 + 1 = 12 + 1 = 13